Srinivani & Spalding (1986)
Srinivani & Spalding propose two shock tubes, solved by changing variables from the conservative unknowns of the conservation equations to stream function and time. The numerical algorithm is by Finite Differences.
First shock tube
In the first case the left half of the tube has higher pressure, the right half has a lower value. Velocity is null and temperature is constant. Derivative of the stream function is null.
In the Gales simulation pressure, temperature and velocity are fixed at the tube ends with the initial values. The problem is solved with the tau 2001 and the 1998 discontinuity capturing version. The time step is 1e-5 s, and the grid resolution is 0.02 m for a total tube length of ~6 m (20 ft).
Fluid properties are defined in props.txt file, initial and boundary conditions are assigned in the fluid_ic_bc.hpp file, while the time step and the stabilization parameters are assigned in the setup.txt file. The simple mesh is built with the mesh.geo file.
Results of velocity, pressure and temperature at 0.05 s (red) are compared successfully with the exact solution (black). Apart from temperature, our computed velocity and pressure behave better than the FD solution (dots).


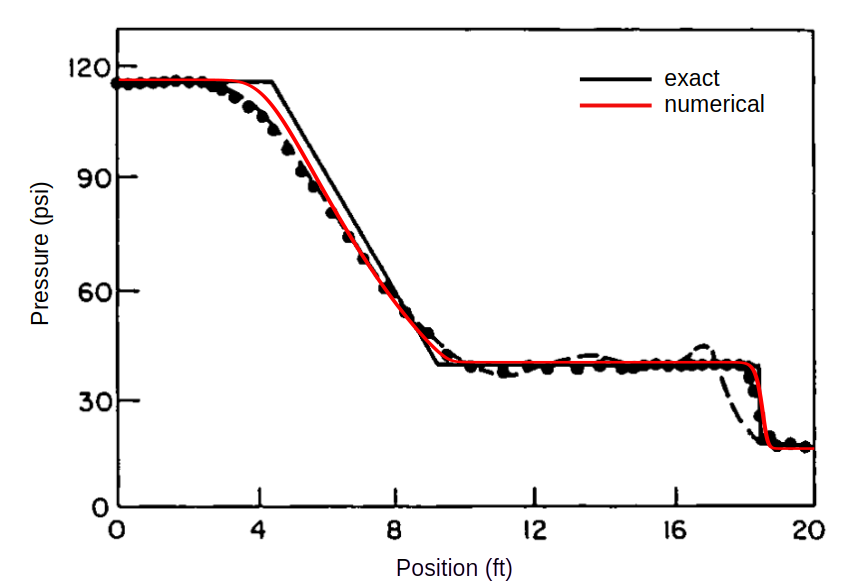
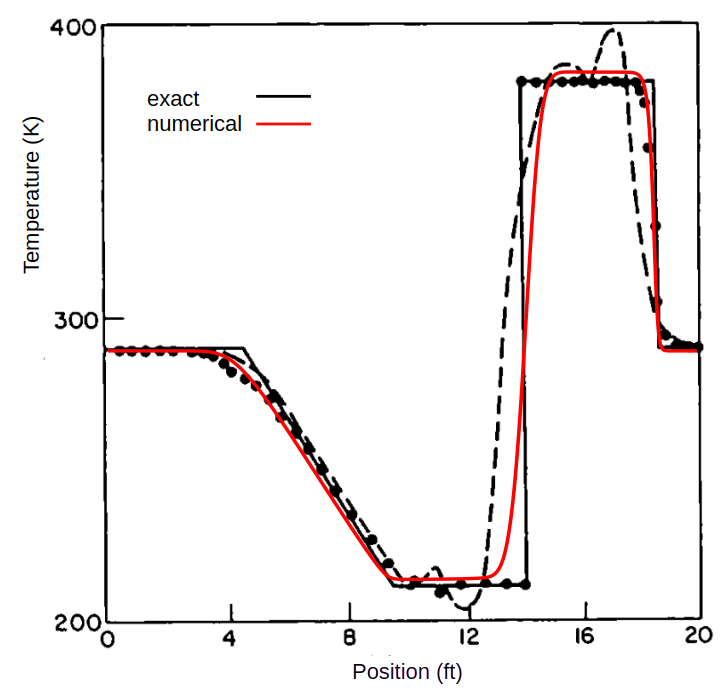
Second shock tube
In the second shock tube the left part is with higher pressure, velocity is null everywhere, and temperature is constant. The ends of the tube are closed.
The benchmark is reproduced by setting longitudinal derivatives of velocity equal to zero and null heat flux. The time step is 1e-5 s, with a grid spacing of 0.01 m.
The stabilization parameters are the tau 2001 and the 1998 discontinuity capturing.
The setting of the simulation is defined in the files props.txt, fluid_ic_bc.hpp, setup.txt and mesh.geo.
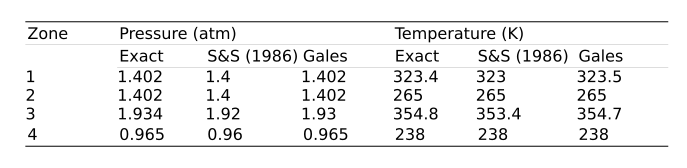
The comparison of the solution obtained with Gales with the results by the authors shows a good agreement as depicted below.

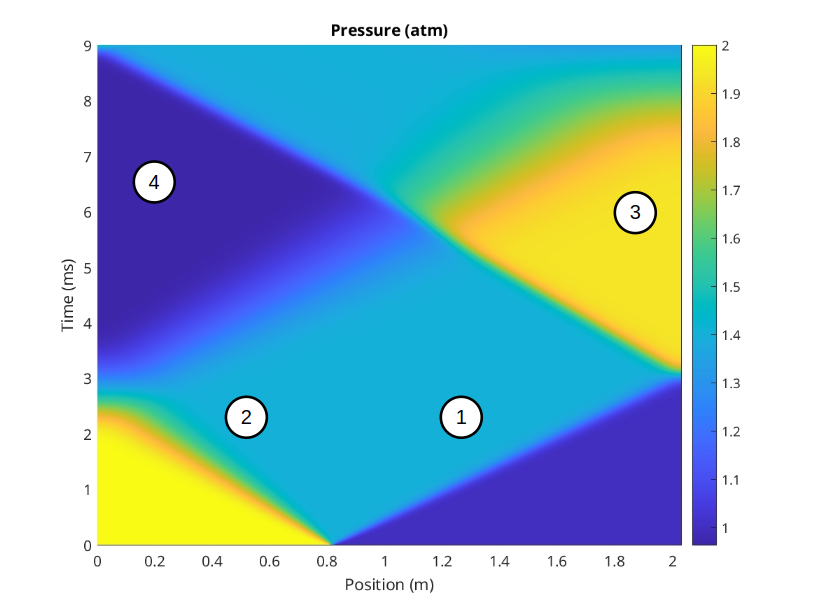
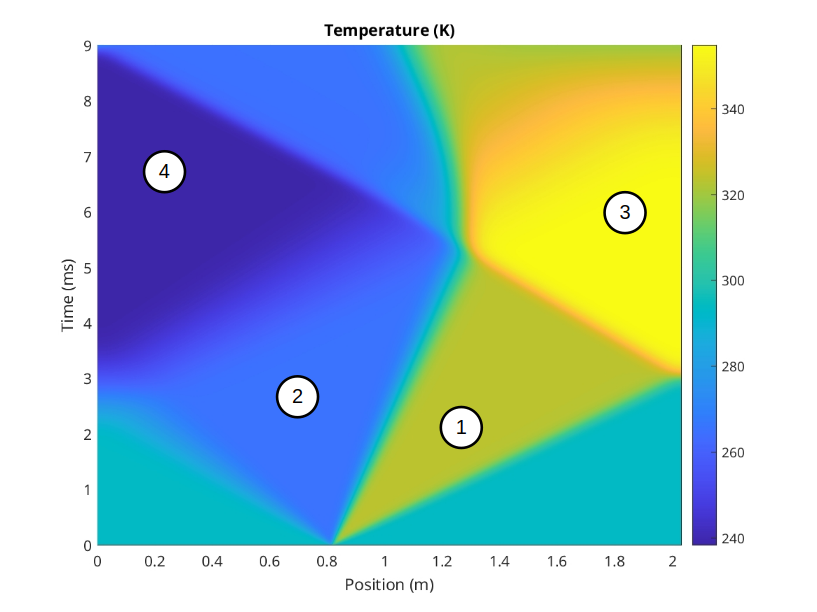
Reference
Srinivasan & Spalding “The stream function coordinate system for solution of one-dimensional unsteady compressible flow problems” (1986) Appl. Math. Modelling
Proudly powered by WordPress
