Fixed cylinder with Re 50

The Fixed Cylinder Benchmark is a classical test problem in computational fluid dynamics and fluid-structure interaction that evaluates the accuracy, stability, and convergence of numerical solvers.

In this benchmark:

• A cylinder is fixed inside a fluid domain (usually a channel), and
• A flow (typically steady or transient) is imposed around it.

The benchmark is important because:

• It creates complex flow features: boundary layers, wake formation, recirculation zones, and possibly vortex shedding.
• It allows for comparison against well-documented reference results for quantities like:
  • Drag and lift coefficients
  • Pressure distribution around the cylinder
  • Velocity profiles at specified cross-sections
  • Wake length and structure
• It tests mesh quality sensitivity, turbulence modeling, and transient solver stability.
• In FSI contexts (with an elastic cylinder), it assesses coupling schemes between fluid and solid solvers.

It provides a controlled, repeatable, and well-studied scenario to validate new numerical methods, codes, or modeling choices before moving to more complex real-world problems.

In the fixed cylinder with Re 50 we investigate the transient development of the laminar flow around the obstacle, under condition of an uniform constant inflow.

The boundary conditions are sketched below, where U = 6.27e-3 m/s:

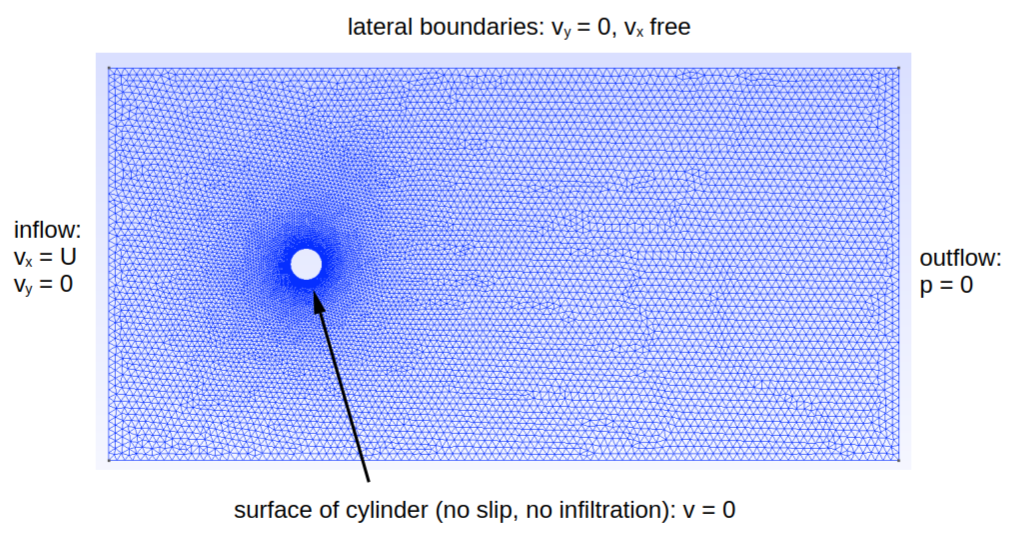
Initial conditions are of null pressure and uniform velocity U.

Initial and boundary conditions are assigned through the fluid_ic_bc.hpp file.

The fluid is incompressible water at 293 K, with density 998.204 kg/m³, and viscosity of 1.002e-3 Pas.

These properties are specified in the props.txt file.

The cylinder diameter is d = 8 mm. The computational region is 50 mm before the cylinder and 150 mm after, for 100 mm in the transversal direction with the cylinder in the middle. Is is discretised with element size of 2e-4 m around the cylinder and 2e-3 m at from the border of the domain. The grid is created with the mesh.geo file.

Computations are performed with 0.01 s of time step, adopting the diagonal incompressible tau of 2007, as prescribed in the setup.txt file.

Results are checked against ” A fundamental study of the flow past a circular cylinder using Abaqus/CFD” by Sato & Kobayashi, 2012 SIMULIA Community Conference.

The developed flow field is illustrated below:

The behavior of the separation of the flow in the rear of the cylinder is studied. The distribution of the velocity vectors in the vicinity of the cylinder are compared below.

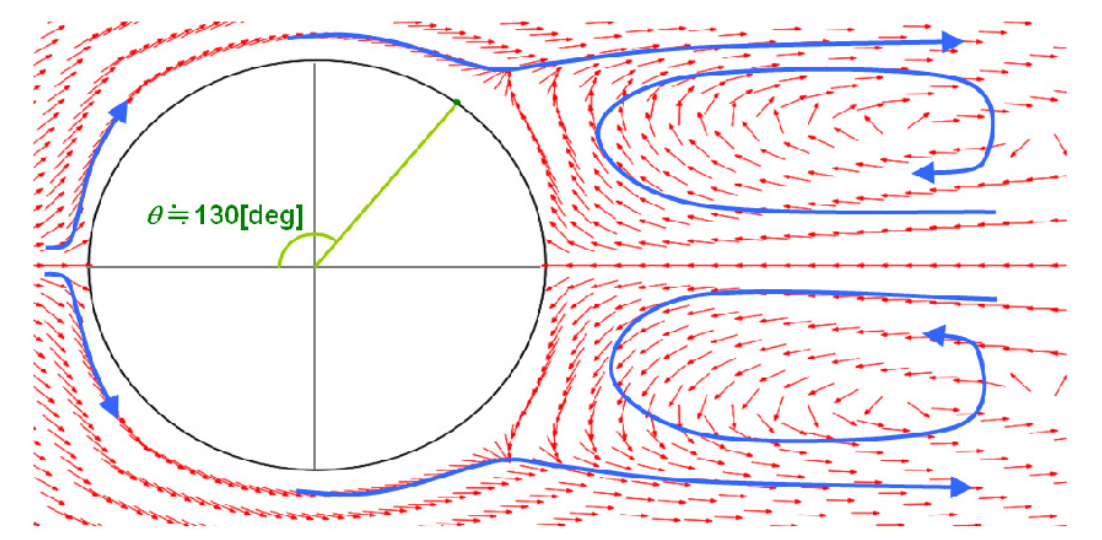
Measuring the angle anticlockwise from the center of the front edge of the cylinder, it is found that the flow begin to separate from the wall surface at an angle of about 130 deg and that reverse flow region forms.

Further, the distributions of the velocities (velocity measured at 0.1 mm from the surface) and pressure at angles from 0 to 180 deg are considered.

As the stagnation point is situated at the front edge of the cylinder, the velocity was zero. The velocity of the cylinder’s front flow accelerates, whereas the velocity of the rear flow decreases. According to Bernoulli’s principle, there is a certain relationship between flow velocity and pressure, with increasing flow velocity resulting decreasing pressure. The resultant pressure distributions conform to this
principle. As the flows moves down-stream and their respective velocities are gradually reduced due to the effects of viscosity and the pressure gradient, the flow can no longer travel along the surface of the cylinder. This phenomenon is called the separation point, which is the point at which the flow is separated from the cylinder’s surface.

Gales velocity results differ from the reference solution, as head of the cylinder velocity is exactly null. This is due to a earlier diverging of the flow in front of the cylinder.