Harmonic response of an elastic rod
This benchmark consists in the perturbation of an elastic rod in the longitudinal direction with a sine function.
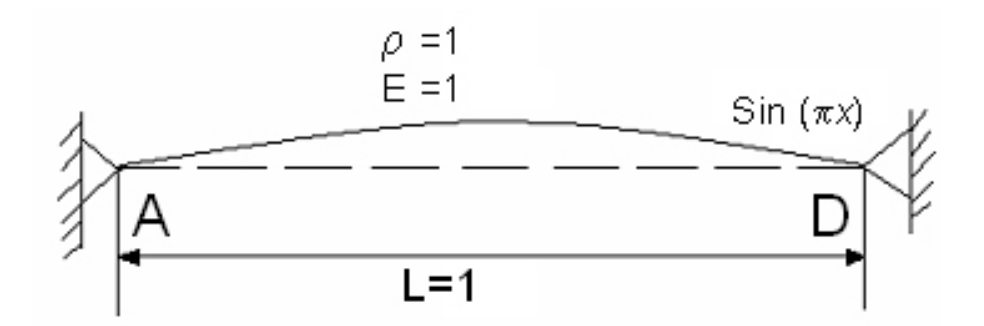
An elastic rod of the length L = 1 is considered. Both ends of the rod are fixed, no external loads are applied, the initial velocity is zero, and the initial displacement is proportional to the first harmonic u(x,0) = sin(π x).
The Young modulus E = 1, and density is 1.
The observation time is T = 20 s.
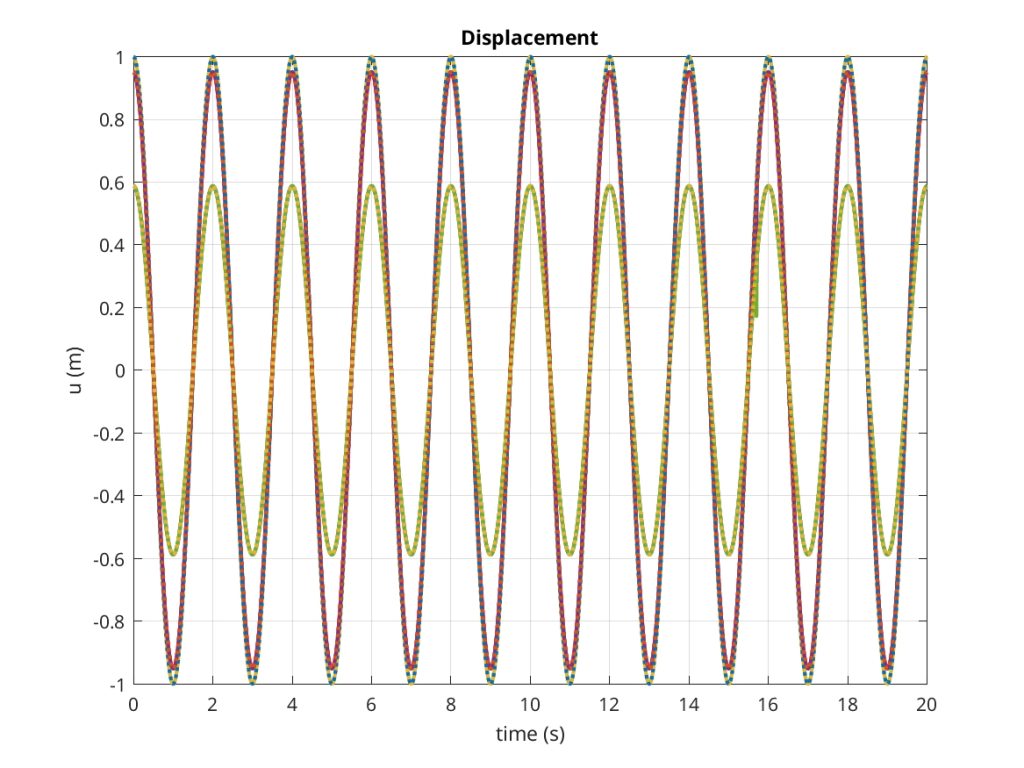
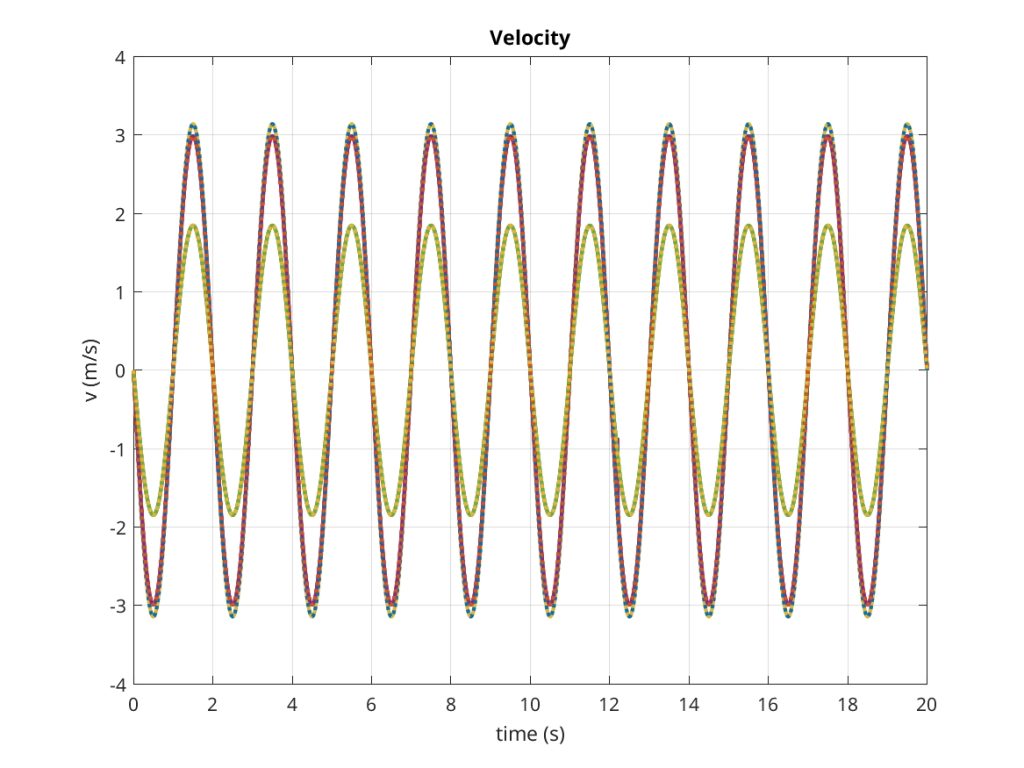
The problem has the continuous analytical solution u(x, t) = sin(π x)cos(π t).
The simulation has been performed setting rho_inf to 0.75, with 1e-4 s of time step, and discretising the rod into 500 regular elements (0.002 m of element size).
Material properties are specified in file props.txt, setting of the numerical solver is defined in file setup.txt, initial and boundary conditions are given in solid_ic_bc.hpp file, while the mesh is constructed by means of the mesh.geo file.
The comparison of exact and computed solution for displacement and velocity are shown below. The computed solution corresponds to the continuous line, while the exact solution is the dashed line.
Reference
Alexander V. Idesman “A new high-order accurate continuous Galerkin method for linear elastodynamics problems” (2007) Computational Mechanics.
Proudly powered by WordPress
