1D impact of an elastic bar against a rigid wall

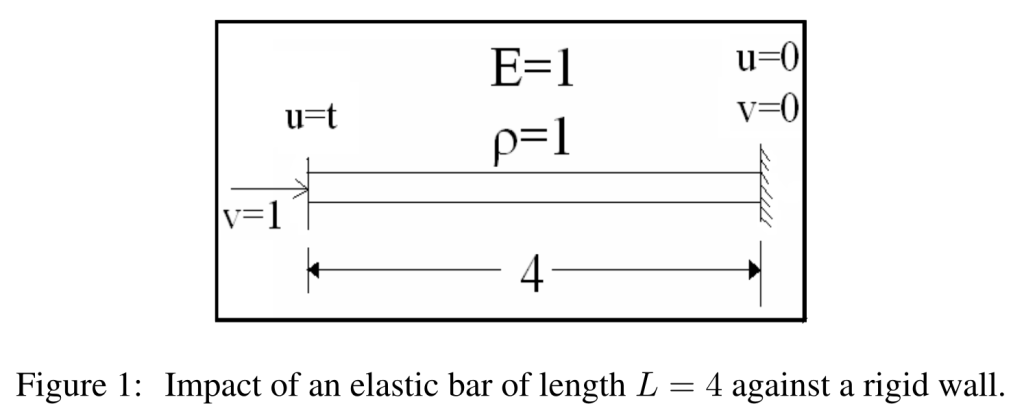
The impact of an elastic bar of the length L = 4 and the cross section A = 1 against a rigid wall is considered in the 1-D case (see Fig. 1). Young’s modulus is chosen to be E = 1 and the density to be ρ = 1.

The following boundary conditions are applied: the displacement u(0,t) = t, which corresponds to velocity v(0,t) = 1, and u(4,t) = 0, which corresponds to velocity v(4,t) = 0. Initial displacements and velocities are null.

The analytical solution to this problem for time 0<t<L sqrt(ρ/E) = 4 includes the continuous variation of displacements u(x,t) = t – x for t>x, and u(x,t) = 0 for t<x; and the piecewise variation of velocity v(x,t) = 1 for t> x and v(x,t) = 0 for t<x. At the interface x = t jump in velocity occurs.

For times 4<t<8 the solution is similar to that for 0<t<4, with the difference that the elastic wave reflects from the right end and propagates to the left. For time 8<t<12 the solution is the same as 0<t<4, and so on.

The generalized alpha method is applied with the parameter ρ_inf = 0.7.

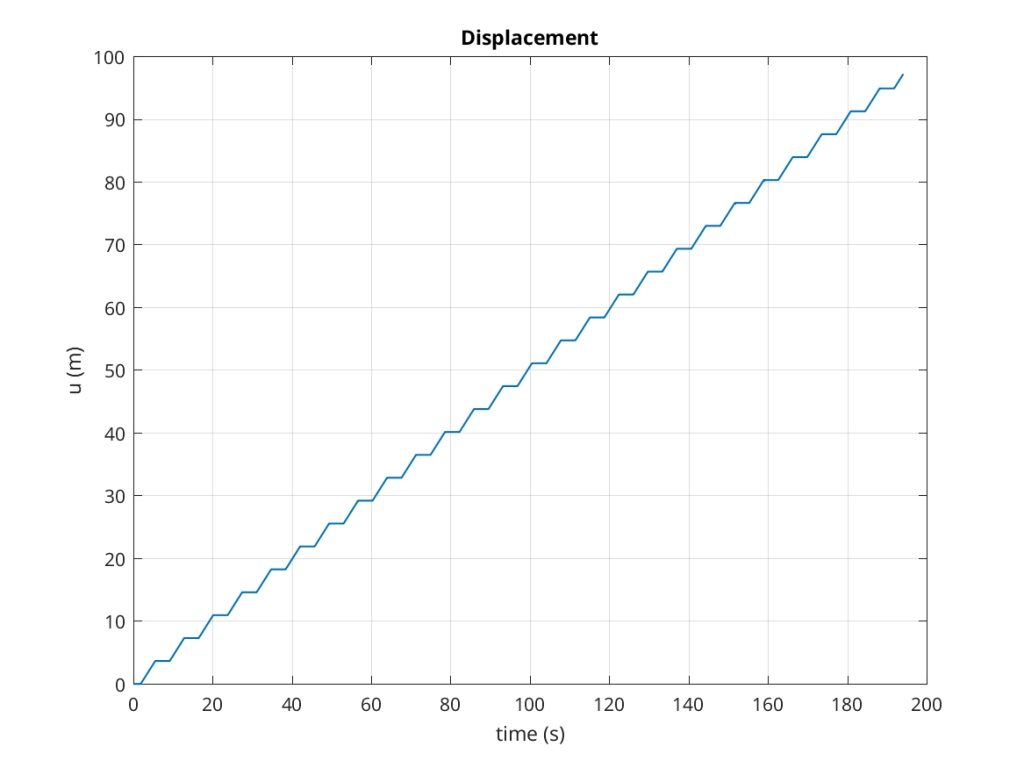
The evolution of displacement and velocity follow.

Reference

Alexander V. Idesman “FINITE ELEMENT MODELING OF LINEAR ELASTODYNAMICS PROBLEMS WITH EXPLICIT TIME-INTEGRATION METHODS AND LINEAR ELEMENTS WITH REDUCED DISPERSION. COMPARATIVE STUDY OF DIFFERENT FINITE ELEMENT TECHNIQUES USED FOR ELASTODYNAMICS.” (2013) 4th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering