Shock reflection

The shock reflection problem was introduced by Shakib et al. (1991) to test the efficiency of the discontinuity capturing operator.

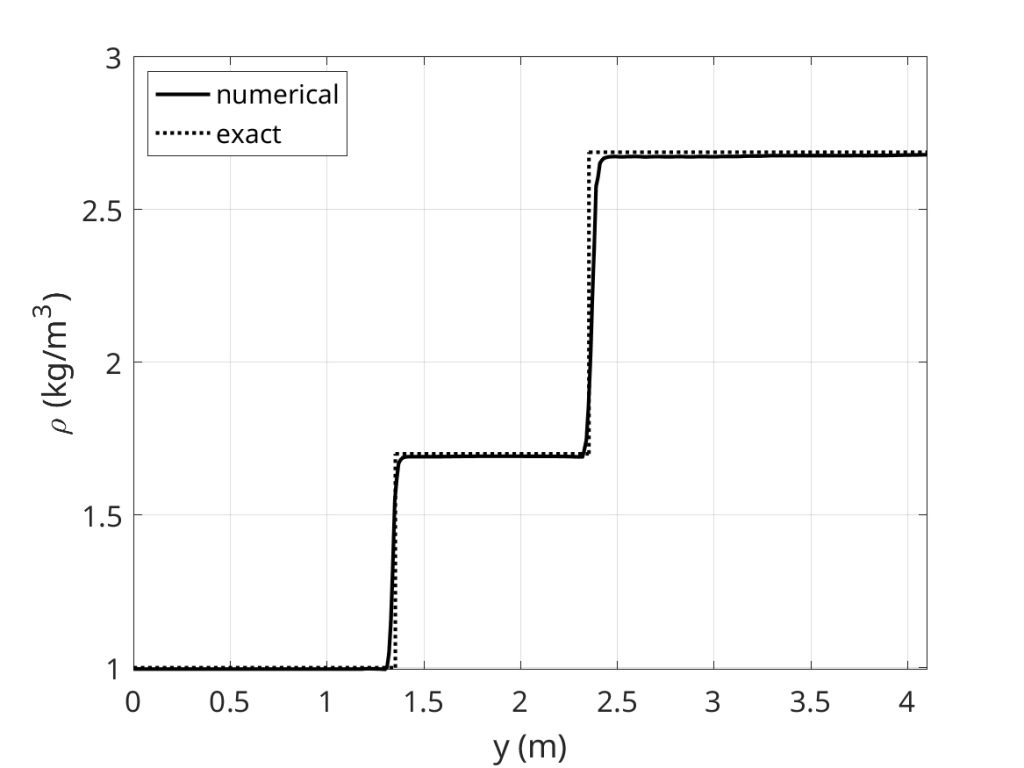
This two-dimensional steady problem consists of three flow regions separated by an oblique shock and its reflection from a wall.

Prescribing the following Mach 2.9 flow data at the inflow (the first region on the left):

Region 1: M=2.9, rho = 1, u = 2.9, v = 0, p = 0.71429

and requiring that the incident shock be at an angle of 29”, leads to the following exact solution:

Region 2: M = 2.3781, rho = 1.7, u = 2.61934, v = -0.50632, p = 1.52819
Region 3: M = 1.94235, rho = 2.68728, u = 2.40140, v = 0, p = 2.93407

In the computations, four flow conditions were imposed on the left and top boundaries; the slip condition was imposed on the wall; and no boundary conditions were imposed on the outflow (right) boundary.

Gales solves the benchmark with the 2001 non-diagonal tau for compressible flows and the 2006 version of the discontinuity capturing operator, with a time step of 0.005 s and a mesh with average element size of 0.01 m. The steady state is definitely reached at 4 s.

All these settings can be found in files setup.txt, props.txt, fluid_ic_bc.hpp, and mesh.geo.

The density values along the line plot well match the exact solution.

Density over the whole domain shows the three flow regions.

References

Shakib et al. (1991) “A new finite element formulation for computational fluid dynamics: X. The compressible Euler and Navier-Stokes equations” CMAME