3D driven cavity

In many industrial, environmental and geophysical ﬂows, the 3D lid-driven cavity ﬂow can be seen as an interesting recirculating ﬂow. The ﬂow is conﬁned in a cubic domain with the upper wall moving at a constant speed. Although the geometry is simple, complex physical phenomena occurs inside the cubic cavity. Contrary to the 2D case, new phenomena can be captured with the 3D simulations. The presence of side-walls conﬁning the full ﬂow modiﬁes the ﬂow pattern so that three-dimensional structures that signiﬁcantly altered the primary ﬂow in the central plane are produced. Recently, the use of three-dimensional numerical simulation becomes a very interesting tool for investigating such physical phenomena in particularly thanks to the increase of technological advances in computer hardware and parallel computing.
A literature review on the 3D problem shows that in fact by examining a plane parallel to the downstream wall, corner eddies were caused at the juncture of the side-walls and the ground while downstream secondary vortices appeared. Moreover, due to centrifugal forces along the downstream, eddy separation surface were found along the span. These vortices are known as Taylor-Görter-like (TGL) vortices in reference to their curvature-induced origins. The number and location of these vortices were also depending on the Reynolds number. The experimental visualization of these vortices were ﬁrst accomplished at Stanford University by Koseff et al.. The numerical prediction of these vortices has to be credited to the work of Freitas et al.. It was mentioned that not only corner vortices in the vicinity of the vertical end-walls were observed but also locally spreading TGL vortices.

The classical setup for the 3D cavity driven is simulated.

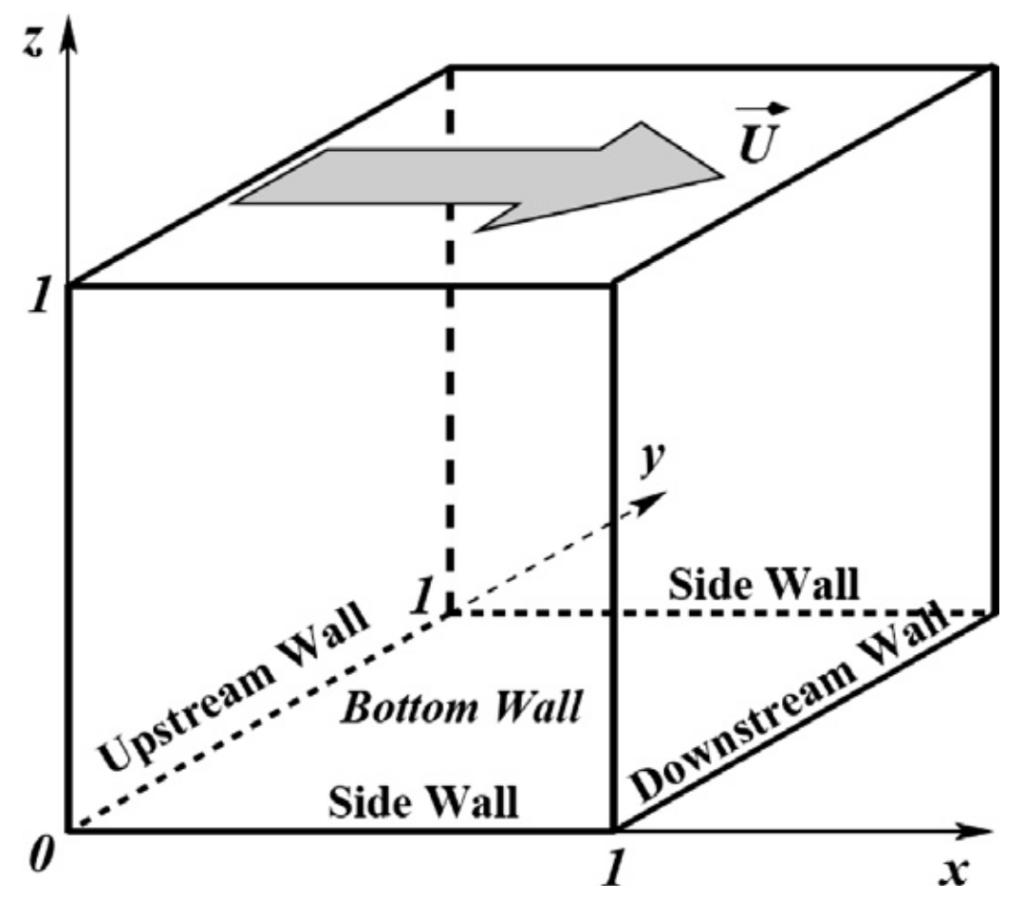
Unit v_x velocity is prescribed at the top plane, while no slip conditions are set on the rest of the boundary of the cubic domain (fluid_ic_bc.hpp). Initial very small (~1e-10) random fields of velocity and pressure are also set.

An incompressible custom fluid with unit density and 1e-3 Pas viscosity is employed (props.txt).

The grid is made of tetrahedrons of 0.02 m average element size (mesh.geo).

The time step is 1e-2 s, and the diagonal tau of 2007 is employed (setup.txt).

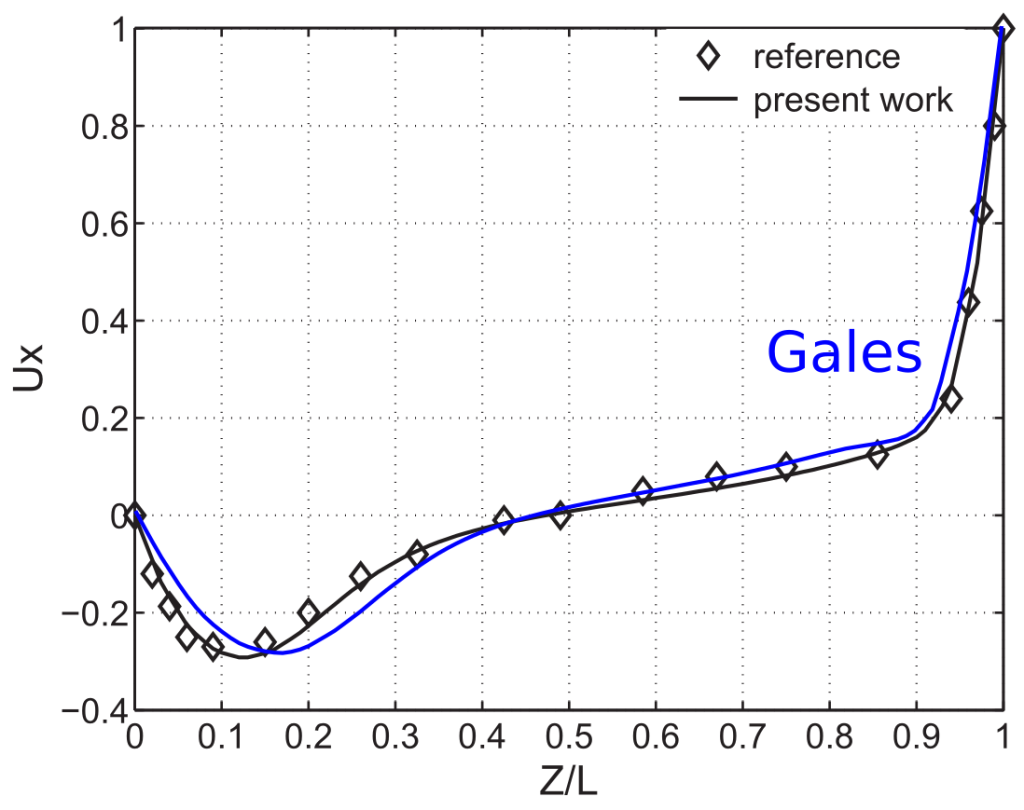
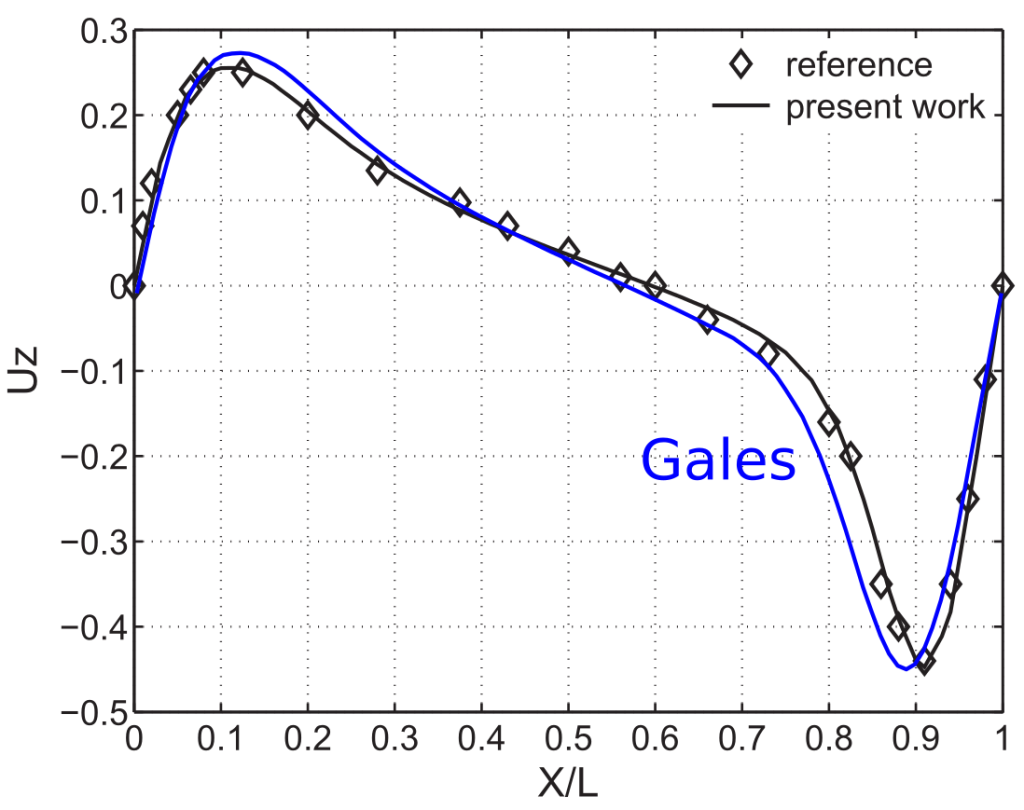
The velocity profiles computed with Gales and the reference solution are shown below.

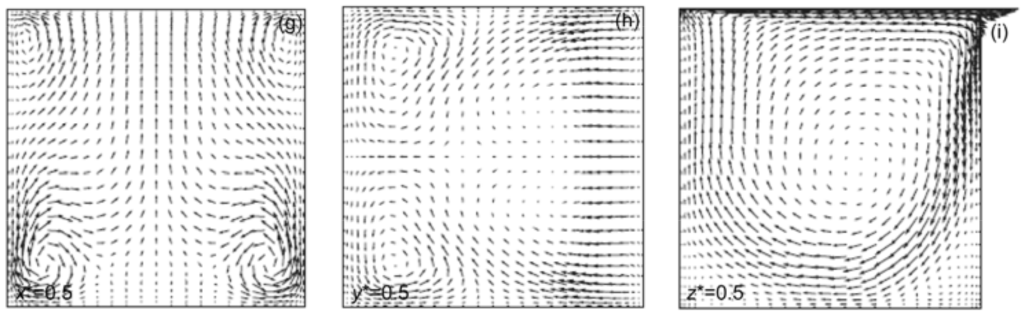
The vector field over the (x,y,z) middle planes is compared with the reference solution below.

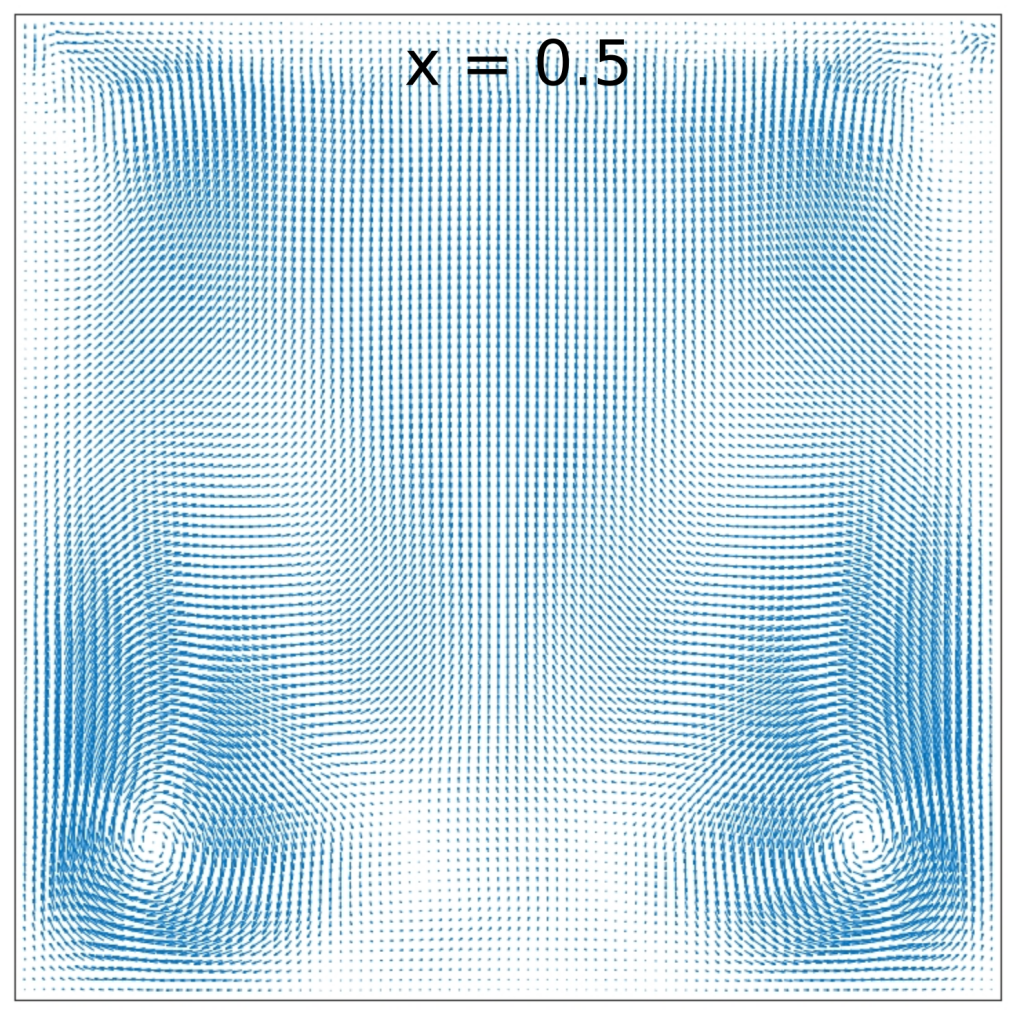
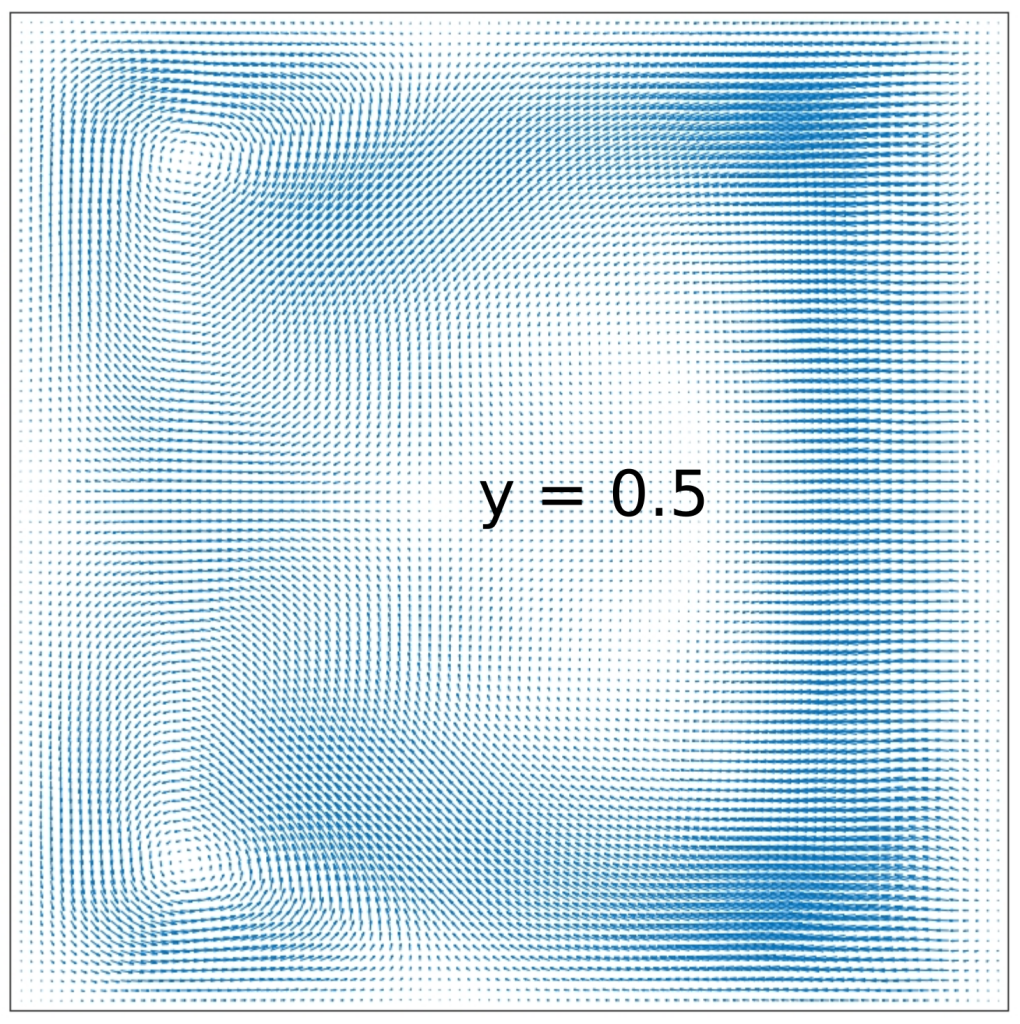
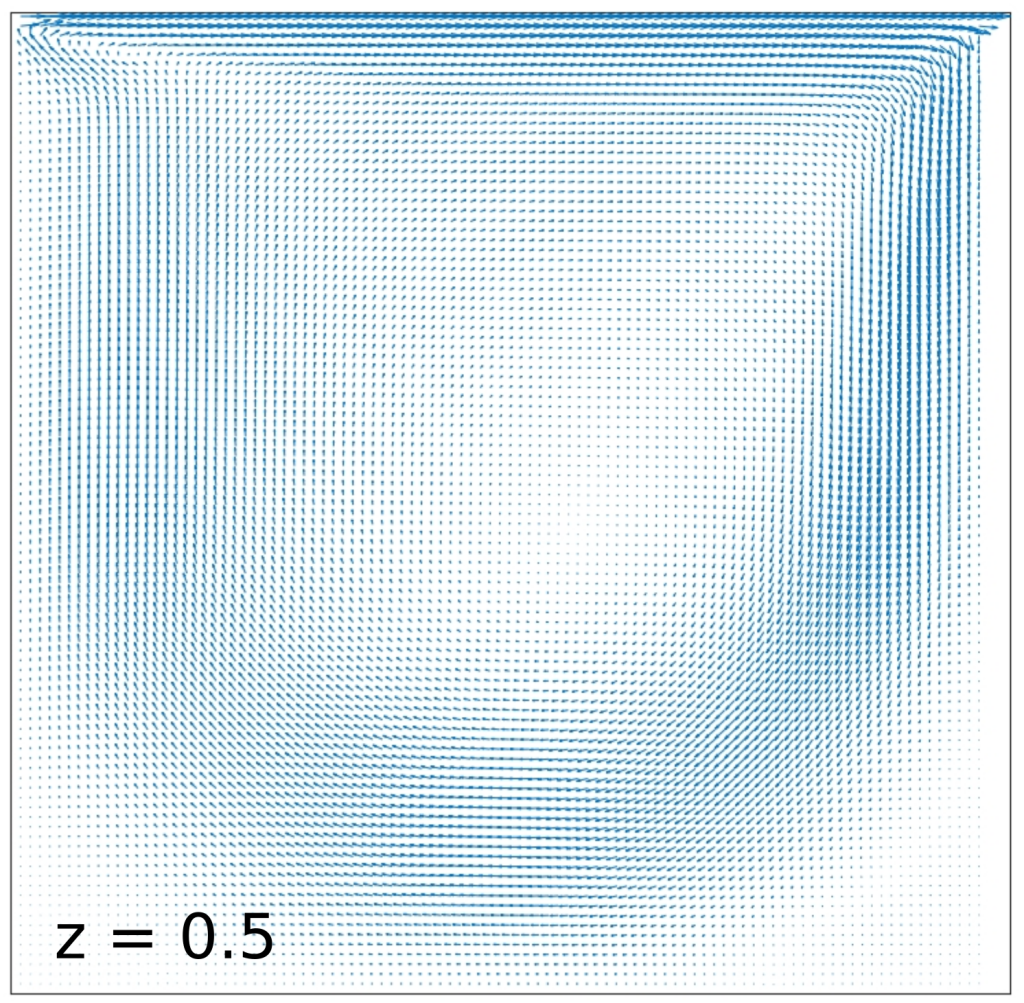
Reference

Hachem et al. “Stabilized ﬁnite element method for incompressible ﬂows with high Reynolds number” (2010) J. Comp. Phy.

XueLin et al. “Numerical research on lid-driven cavity flows using a three-dimensional lattice Boltzmann model on non-uniform meshes” (2013) Sci China Tech Sci